Learning equations for ocean turbulence using machine learning

Neural Nets + Physics vs. Equation-discovery for parameterization

Our new work with Tom Bolton on physics-aware & interpretable ML to improve ocean models is out in GRL.

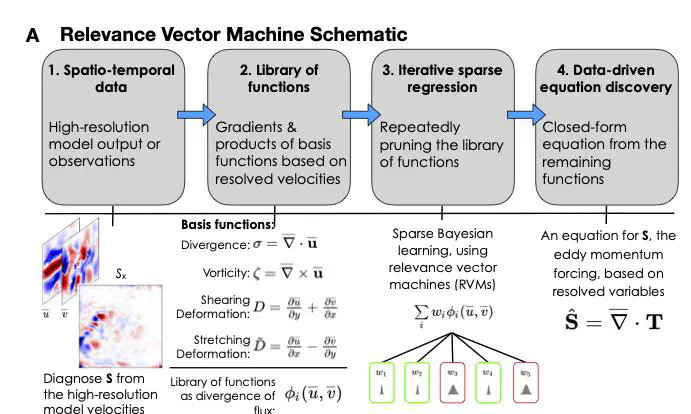
Our new approach to the parameterization/closure problem: learning differential equations of missing physics in coarse-res ocean models from data. We use a machine learning (ML) method that relies on sparse Bayesian inference / relevance vector machine to learn ocean eddy parameterizations of momentum, buoyancy, and energy. We compare it to a ML parameterization which uses convolutional neural nets with conservation-law embedded in the architecture. Each approach has pros and cons (interpretability, generalization, numerical stability) in our proof-of-concept. Many aspects need to be improved but we are moving one step closer towards blending physics and machine learning for climate modeling.